Power-Law Compensator Design for Plants with Uncertainties: Experimental Verification
Abstract
:1. Introduction
2. Power-Law Compensator for Robustness against Plant Uncertainty
2.1. Theory
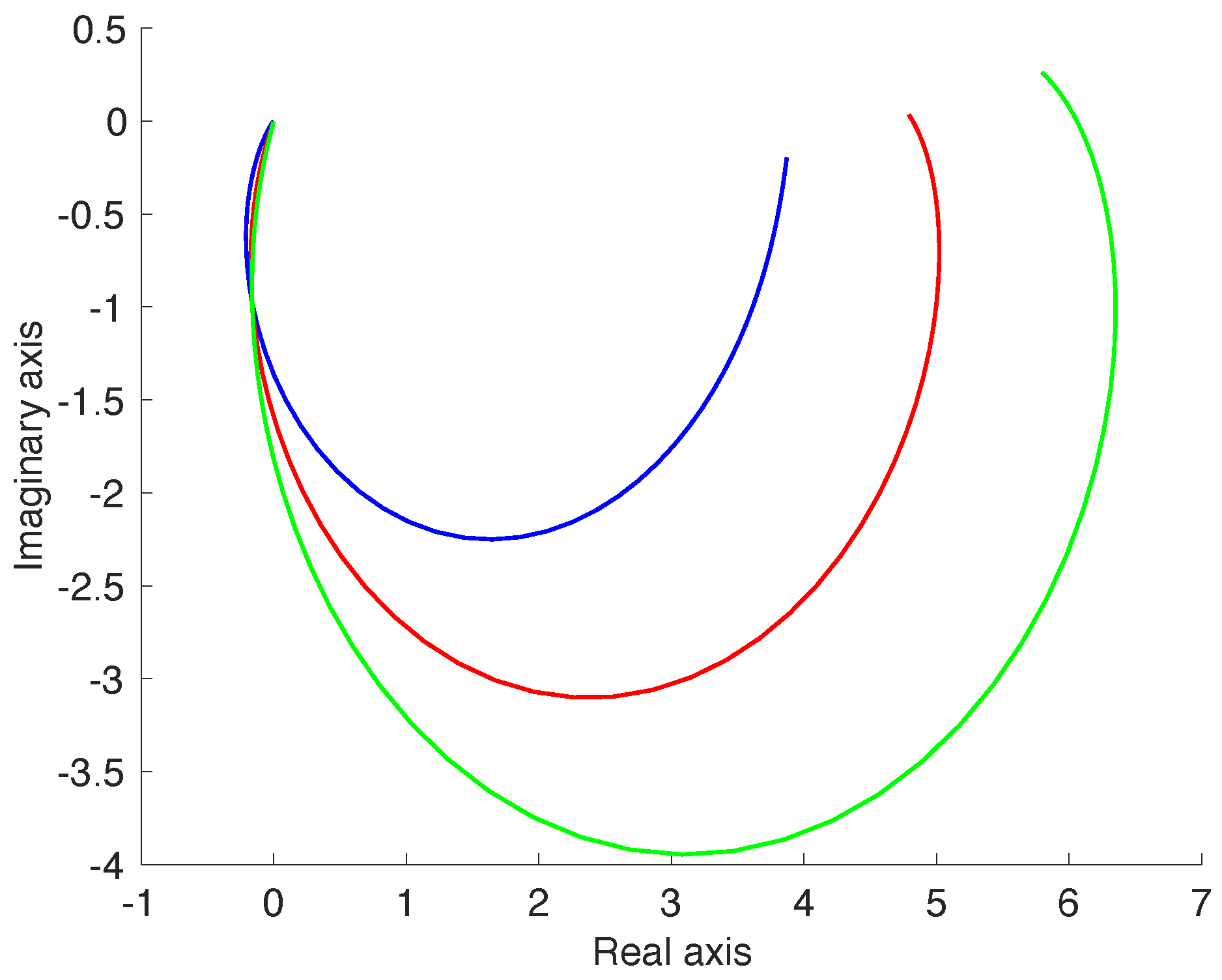
- In the nominal case (i.e., ), the Nyquist diagram of the open-loop transfer function meets the fixed point , where and , at a desired frequency ;
- Despite the variations of b from its nominal value, the Nyquist diagram of the transfer function still crosses the fixed point .
2.2. Design Example
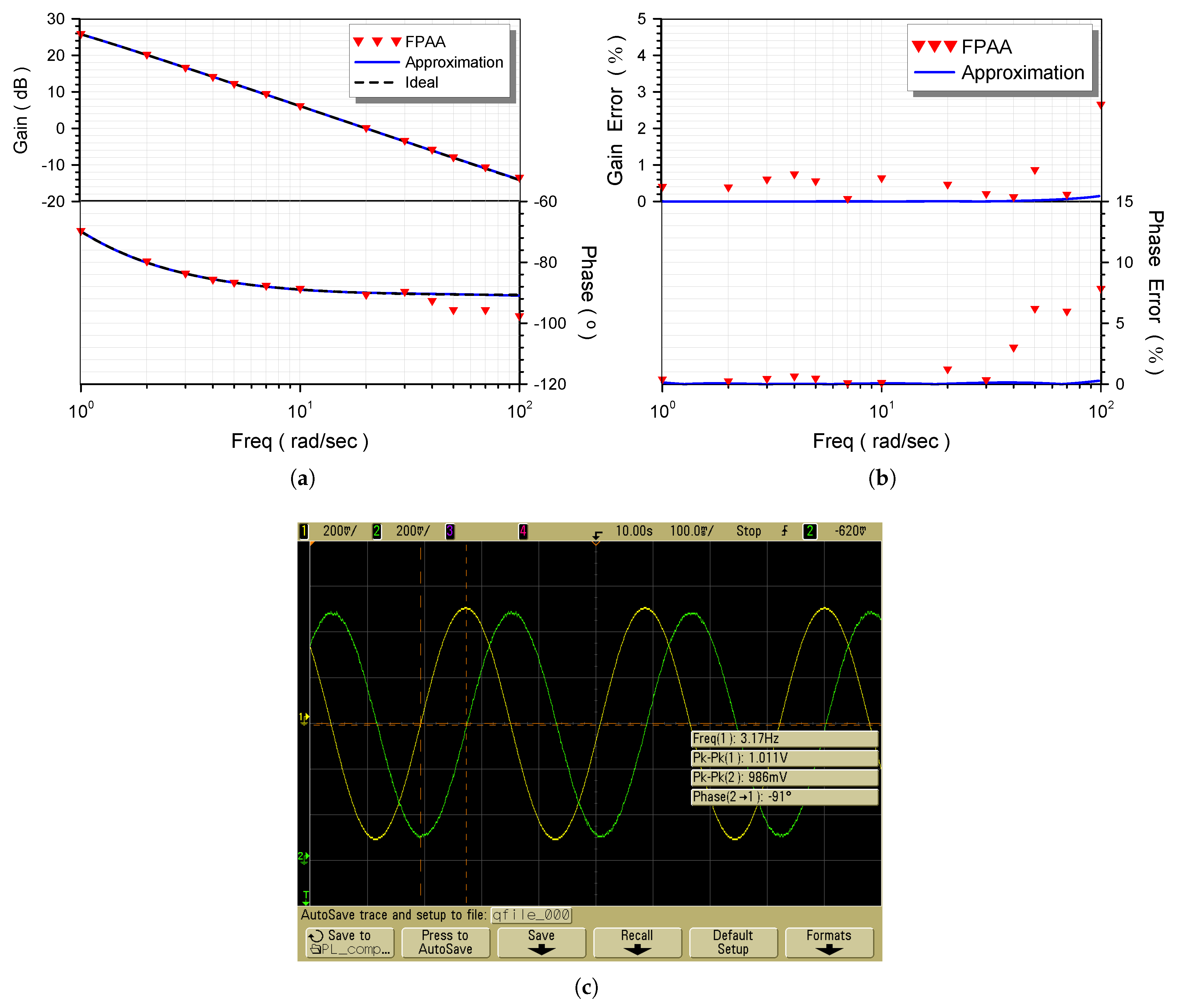
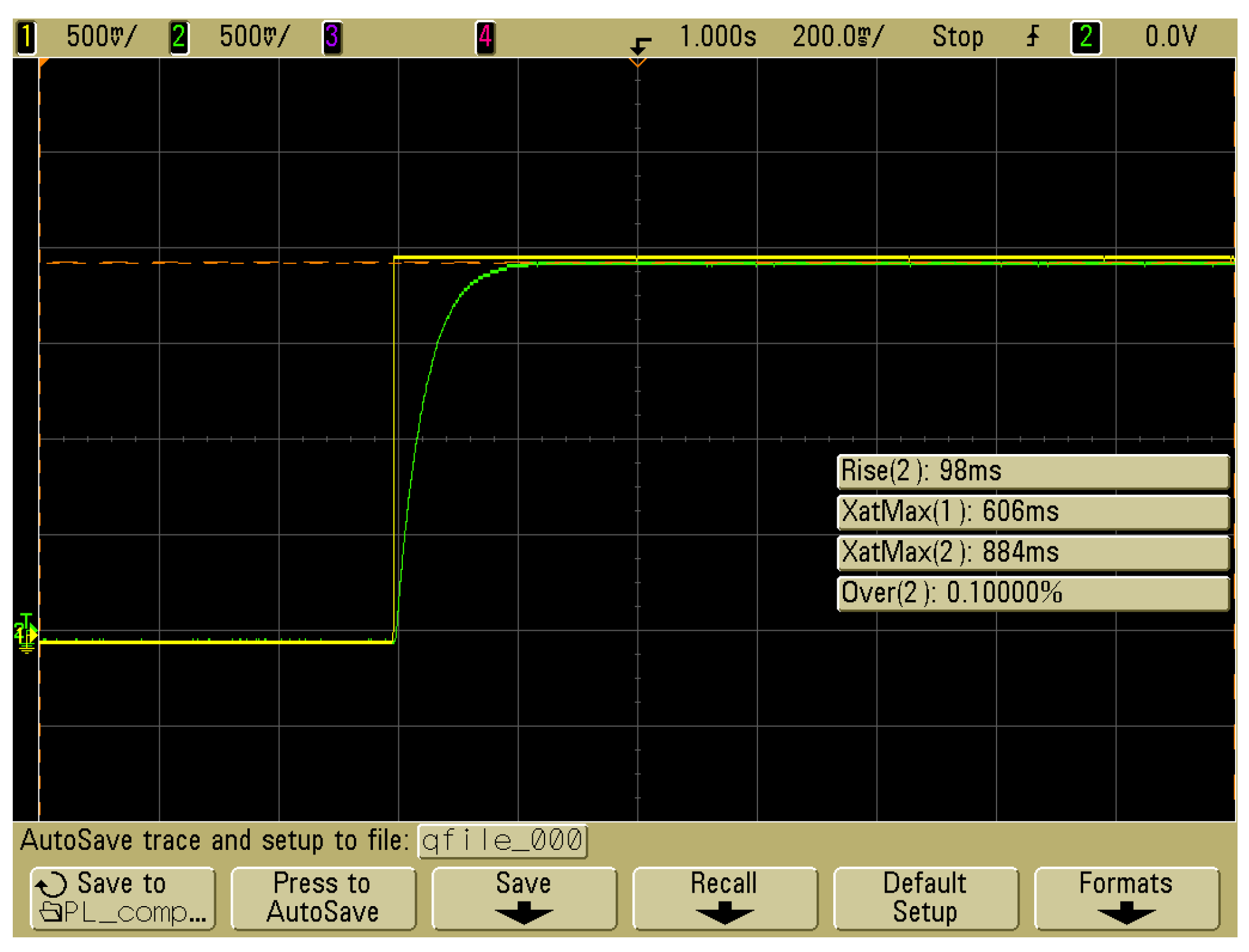
3. Experimental Verification
3.1. Compensator-Plant System
3.2. Effect of the Plant Uncertainties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAB | Configurable analog block |
| FLF | Follow the leader feedback |
| FPAA | Field programmable analog array |
| IFLF | Inverse follow the leader feedback |
| FBD | Functional block diagram |
| PM | Phase margin |
References
- Caponetto, R.; Dongola, G.; Maione, G.; Pisano, A. Integrated technology fractional order proportional-integral-derivative design. J. Vib. Control 2014, 20, 1066–1075. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; García-Jiménez, L.V.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. New alternatives for analog implementation of fractional-order integrators, differentiators and PID controllers based on integer-order integrators. Nonlinear Dyn. 2017, 90, 241–256. [Google Scholar] [CrossRef]
- Dimeas, I.; Petras, I.; Psychalinos, C. New analog implementation technique for fractional-order controller: A DC motor control. AEU Int. J. Electron. Commun. 2017, 78, 192–200. [Google Scholar] [CrossRef]
- Tavakoli-Kakhki, M.; Haeri, M.; Tavazoei, M.S. Simple fractional order model structures and their applications in control system design. Eur. J. Control 2010, 16, 680–694. [Google Scholar] [CrossRef]
- Tavazoei, M.S. Time response analysis of fractional-order control systems: A survey on recent results. Fract. Calc. Appl. Anal. 2014, 17, 440–461. [Google Scholar] [CrossRef] [Green Version]
- Padula, F.; Visioli, A. Advances in Robust Fractional Control; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Luo, Y.; Chen, Y. Fractional-order [Proportional Derivative] controller for robust motion control: Tuning procedure and validation. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1412–1417. [Google Scholar]
- Luo, Y.; Chen, Y.Q.; Wang, C.Y.; Pi, Y.G. Tuning fractional order proportional integral controllers for fractional order systems. J. Process. Control 2010, 20, 823–831. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y. Stabilizing and robust fractional order PI controller synthesis for first order plus time delay systems. Automatica 2012, 48, 2159–2167. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, T.; Lee, B.; Kang, C.; Chen, Y. Fractional-order proportional derivative controller synthesis and implementation for hard-disk-drive servo system. IEEE Trans. Control Syst. Technol. 2013, 22, 281–289. [Google Scholar] [CrossRef] [Green Version]
- Basiri, M.H.; Tavazoei, M.S. On robust control of fractional order plants: Invariant phase margin. J. Comput. Nonlinear Dyn. 2015, 10, 054504. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Saikumar, N.; HosseinNia, S.H. Tuning guidelines for fractional order PID controllers: Rules of thumb. Mechatronics 2018, 56, 26–36. [Google Scholar] [CrossRef]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.; HosseinNia, S.H. Linear fractional order controllers; A survey in the frequency domain. Annu. Rev. Control 2019, 47, 51–70. [Google Scholar] [CrossRef]
- Li, X.; Gao, L. Robust Fractional-order PID Tuning Method for a Plant with an Uncertain Parameter. Int. J. Control Autom. Syst. 2021, 19, 1302–1310. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.A.; Hosseinnia, S.H.; Petlenkov, E.; Ates, A.; Cech, M. Towards Industrialization of FOPID Controllers: A Survey on Milestones of Fractional-Order Control and Pathways for Future Developments. IEEE Access 2021, 9, 21016–21042. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, Y.Q.; Xue, D. Time-constant robust analysis of a fractional order [proportional derivative] controller. IET Control Theory Appl. 2011, 5, 164–172. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Castillo-García, F.J. On the robust control of stable minimum phase plants with large uncertainty in a time constant. A fractional-order control approach. Automatica 2014, 50, 218–224. [Google Scholar] [CrossRef]
- Sayyaf, N.; Tavazoei, M.S. Robust fractional-order compensation in the presence of uncertainty in a pole/zero of the plant. IEEE Trans. Control Syst. Technol. 2018, 26, 797–812. [Google Scholar] [CrossRef]
- Basiri, M.H.; Tavazoei, M.S. Robust Control of a Class of Fractional Order Plants in the Presence of Pole Uncertainty. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on, Mashhad, Iran, 8–10 May 2018; pp. 881–886. [Google Scholar]
- Sayyaf, N.; Tavazoei, M.S. Desirably adjusting gain margin, phase margin, and corresponding crossover frequencies based on frequency data. IEEE Trans. Ind. Inform. 2017, 13, 2311–2321. [Google Scholar] [CrossRef]
- Sayyaf, N.; Tavazoei, M.S. Frequency data-based procedure to adjust gain and phase margins and guarantee the uniqueness of crossover frequencies. IEEE Trans. Ind. Electron. 2020, 67, 2176–2185. [Google Scholar] [CrossRef]
- Sommacal, L.; Melchior, P.; Oustaloup, A. Havriliak-Negami function for thermal system identification. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 1316–1321. [Google Scholar]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator. AEU Int. J. Electron. Commun. 2021, 129, 153537. [Google Scholar] [CrossRef]
- Kapoulea, S.; Tsirimokou, G.; Psychalinos, C.; Elwakil, A.S. Employment of the Padé approximation for implementing fractional-order lead/lag compensators. AEU Int. J. Electron. Commun. 2020, 120, 153203. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Double Exponent Fractional-Order Filters: Approximation Methods and Realization. Circuits Syst. Signal Process. 2021, 40, 993–1004. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. On the electronic realizations of fractional-order phase-lead-lag compensators with OpAmps and FPAAs. In Fractional Order Control and Synchronization of Chaotic Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 131–164. [Google Scholar]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Anadigm. AN231E04 dpASP: The AN231E04 dpASP Dynamically Reconfigurable Analog Signal Processor; Anadigm: Mesa, AZ, USA, 2021. [Google Scholar]




| Time Constants | Scaling Factors | |||||
|---|---|---|---|---|---|---|
| 4.9 ms | 53.3 ms | 497.7 ms | 13.235 | |||
| Time Constants | Scaling Factors | |||||
|---|---|---|---|---|---|---|
| 77.1 ms | 742.1 ms | 3.558 s | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapoulea, S.; Psychalinos, C.; Elwakil, A.S.; Tavazoei, M.S. Power-Law Compensator Design for Plants with Uncertainties: Experimental Verification. Electronics 2021, 10, 1305. https://doi.org/10.3390/electronics10111305
Kapoulea S, Psychalinos C, Elwakil AS, Tavazoei MS. Power-Law Compensator Design for Plants with Uncertainties: Experimental Verification. Electronics. 2021; 10(11):1305. https://doi.org/10.3390/electronics10111305
Chicago/Turabian StyleKapoulea, Stavroula, Costas Psychalinos, Ahmed S. Elwakil, and Mohammad Saleh Tavazoei. 2021. "Power-Law Compensator Design for Plants with Uncertainties: Experimental Verification" Electronics 10, no. 11: 1305. https://doi.org/10.3390/electronics10111305









